-
Compiling Numpy With Atlas
Numpy is a great python package for scientific computing. Although it comes with many performant functions and the ability to vectorise your own functions, it is sometimes necessary to distribute your code across multiple cores.
-
Cpp Containers In Cython
Cython’s typed memoryviews provide a great interface for rectangular arrays. But I often need to represent jagged arrays such as the neighbours of nodes in a network. The standard python dictcan represent such data nicely but is not statically typed. It can thus be quite slow compared with the templated containers in the C++ standard library. In this post, we’ll have a look at how to use the power of the STL via cython. -
Variational Linear Regression In Tensorflow
We discussed some of the problems with the variational mean-field optimisation algorithms in a previous post, and showed that the optimisation problem can be solved using the machine learning library theano. Let’s try to do the same usingtensorflow, which provides a nice optimisation interface. -
Oscillating Parameters In Variational Mean Field Approximation
Variational Bayesian methods are a great way to get around the computational challenges often associated with Bayesian inference. Because the posterior distribution is often difficult to evaluate, variational methods approximate the true posterior by a parametric distribution with known functional form. The inference algorithm is thus reduced to an optimisation problem whose objective is to tune the parameters of the approximate distribution to match the posterior. Using the popular mean-field approximation, guarantees that the EM-like updates increase the evidence lower bound (ELBO) with every iteration. However, the values of the variational parameters can oscillate if they are strongly coupled by the posterior distribution. The resulting slow convergence is often not obvious from monitoring the ELBO. In this post, we illustrate the problem using a simple linear regression model, and consider alternatives that can help to fit Bayesian models using variational approximations. -
Unified Treatment Of The Asymptotics Of Asymmetric Kernel Density Estimators
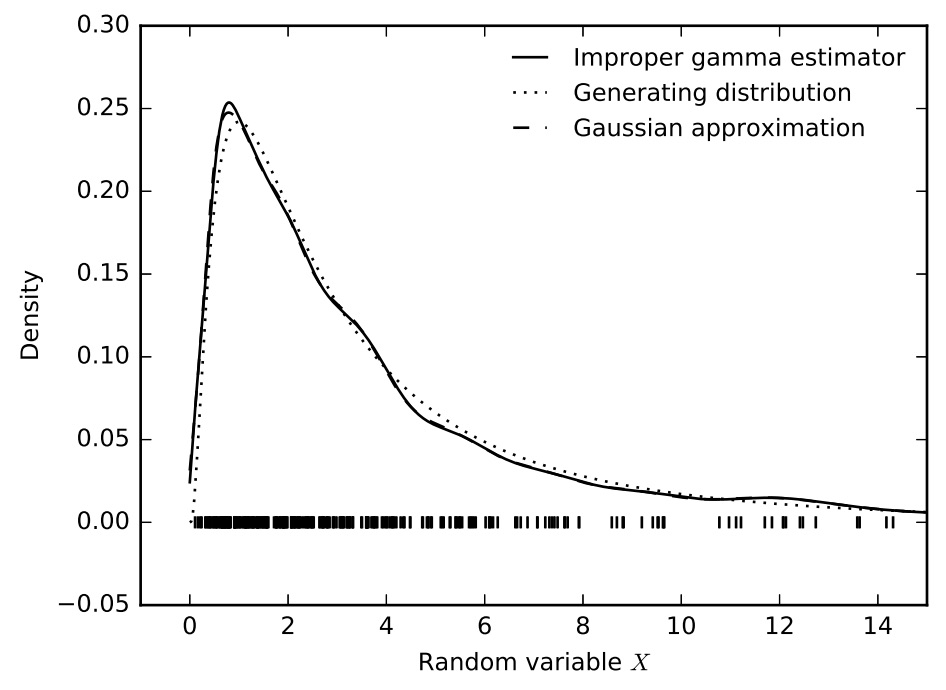We extend balloon and sample-smoothing estimators, two types of variable-bandwidth kernel density estimators, by a shift parameter and derive their asymptotic properties. Our approach facilitates the unified study of a wide range of density estimators which are subsumed under these two general classes of kernel density estimators. We demonstrate our method by deriving the asymptotic bias, variance, and mean (integrated) squared error of density estimators with gamma, log-normal, Birnbaum-Saunders, inverse Gaussian and reciprocal inverse Gaussian kernels. We propose two new density estimators for positive random variables that yield properly-normalised density estimates. Plugin expressions for bandwidth estimation are provided to facilitate easy exploratory data analysis.